SPARE TRANSFORMERS

Spare transformers are kept in stock so that failed units can be replaced relatively quickly.  Absent a spare, most large power transformers have a replacement or repair time of at least 9 – 12 months.  On the transmission system, failure of one transformer will not result in service interruption, but during the long replacement time the power system is at risk of a second failure occurring.  This can affect load-serving capability, and inter-regional power transfer capability.

On the distribution system, the situation is a bit different, but spares still have an important role.  The distribution substations typically have multiple transformers, and at most utilities monitoring and planning is carefully performed to ensure that substation loads do not exceed the “firm” N-1 rating of the substation.  In the case of single-transformer substations’ exposure to transformer failure, either adequate feeder ties to other substations are provided, or a mobile transformer is kept is stock.

Mobiles are practical for transformers up to about 50 MVA; beyond that the sizes and weights become impractical.  Mobiles have the advantage of fast installation, but do not address the need for a permanent replacement; hence spares are also relevant for distribution system transformers, just as for transmission transformers.

At large utilities, the transmission transformers may be of many different voltage combinations, and of different sizes within each combination.  For example, there may be two or three sizes of 345/115 kV transformer, and four or five sizes of 115/69 kV transformer.   There will often also be a few “one or two of a kind” combinations on the system.  Due to the size, cost, and reliability impact of these transmission transformers, proper determination of spares inventory is an important activity.

On the distribution side of the house there may be hundreds of transformers, but typically of just a few voltage combinations, although of varying MVA capacity.  Most large utilities will have “35 kV”, “25 kV” and “15 kV-class” distribution systems, and multiple transmission supply voltages (69, 115, 138, 161, and 230 kV).  This results in many possible combinations of primary and secondary voltage, although not all combinations of high-side and low-side voltages may exist on a particular system.  Considering both the various voltage combinations and the several transformer capacities, provision of spares for the distribution transformers is a non-trivial exercise. 

How to do it correctly 

We need to look at probability of occurrence, replacement time, and cost.

Probability of occurrence (# of failures/yr) is simply the individual transformer failure rate, times the number of units in service.  In the real word, however, it works the other way around:  we don’t know individual failure rates, but do have experience with overall failure rate for the fleet.  If during the past 30 years we’ve had 20 transformers of a particular type, and there have been 3 failures, we reckon that the individual unit annual failure rate is 3 failures/600 tx-years = 1 failure per 200 tx-years, or 0.5%.

Replacement time is relevant because it strongly influences the probability of two or more outages overlapping in time.  If the replacement time (no spare) is 12 months, but having a spare on hand reduces this to 1 month, the probability of having 2 or more transformers simultaneously out of service is significantly reduced, although not exactly in the ratio 1:12, as one might at first expect.   The resultant reduction is somewhat less, because the original higher-order (N-3, N-4, N-5) probabilities contribute to the revised N-1, N-2, and N-3 probabilities.

The correct way of taking into account both the probability of occurrence of failure(s) and replacement time is to compute the probability of the various possible system states (N-0, N-1, N-2, N-3, etc.) by having the failure rates expressed on the same interval as the replacement time.  For example, if the replacement time is 12 months, you need to compute the probabilities for N-0, N-1, etc. using the individual transformer failure rate expressed on a 12-month base.  If the replacement time is 9 months, the rates must be expressed on a 9-month base.

Computation of the N-0, N-1, N-2, etc. state probabilities is easily done using the Binomial Probability Distribution Function (BPDF) formula.   This is the correct method because this is a go/no-go situation, the failure rate is constant, and the failures are independent of each other (but possibly overlapping).  Technically, we’re dealing with a Bernoulli random variable; this is precisely what the BPDF models, exactly.

Cost of having a spare in stock is a relevant concern because it may not be optimal to have a spare for each particular voltage/MVA combination.  It may be more economical for one spare to cover more than one combination.  For example, suppose a system has the following distribution transformers:

#              MVA

20               25

60               50

45               70

In this instance it may be advantageous to skip having a 25 MVA spare, and just use the 50 MVA spare when a 25 MVA unit fails.  Although some transformer capacity is wasted by installing a 50 MVA  unit where a 25 MVA unit would be adequate, the long-term cost of this occasional waste of capacity may be less than the cost of having a rarely-used 25 MVA unit continuously in stock. 

Common pitfalls

It is easy to make the analysis method unnecessarily complex, and it is easy to acquire and use bad data.  The result can be a difficult-to-understand method that yields spurious results.

One large utility was proud of having developed a very complex “Monte Carlo” model where each class and size of transformer was explicitly modeled, and each voltage combination had a different failure rate, supposedly based on actual field experience.  This model was yielding results that largely made little sense, although the method appeared to be mathematically correct.

The problems were several:

• It was incorrect to expect that the failure rates should be different for distinct (but similar) transformer classes.  Think about it for a moment:  if the 115-12.5 kV and the 115-13.8 kV transformers are all purchased under the same specification, from the same manufacturers, using similar designs, constructed at the same factories, with the same workers using the same materials and tools, and installed in similar substations where they are exposed to similar conditions, what reason is there to believe the in-service failure rates might differ to a large degree?

• The failure rates were not computed from a list of failed transformers, but were instead inferred from inventory records.  If an in-service transformer had been removed from the pad, and not re-installed elsewhere, or kept in stock, it was deemed to have been a failure.  This definition of “failure” resulted in a significant over-estimation of failure rate because

1. The inventory records were not accurate.  Some transformers were re-used    elsewhere, but the later re-use did not get correlated to the original removal.  These units were incorrectly counted as “failures”.
2. Some transformers were removed from service and scrapped due to obsolescence, rather than failure.  If you’re in the process of retiring all the 13-4 kV substations, you scrap most of those old transformers, even though they work fine.  Similarly, if an old 115/69 kV transformer is too small to re-use anywhere, it gets scrapped.  These scrapped units were incorrectly identified as failures.

The practice of counting “scrapping” as a failure was defended by some of the utility staff through the interesting argument that if a transformer was old and hadn’t failed yet, it would have soon anyway, so it should be counted as a failure.  The fallacy of this reasoning is easily shown:

• Suppose the actual annual failure rate of the transformers is 1%.  This means that the individual transformers will fail, on average, about once every 100 years.  Suppose, however, that the transformers are scrapped at an average age of 50 years, due to obsolescence.  If all the units that are scrapped are counted as failures, the failure rate will be calculated as once every 50 years, or 2%, even if no failures have actually occurred.  But this result contradicts the knowledge that the actual failure rate is only 1%.  This method is obviously incorrect.

The overall result of this utility’s data collection practices and the modeling method used was to produce a significant general over-statement of failure rates, and to produce a remarkably wide range of failure rates among the different transformer classes.  The “optimal” set of spares and mobiles was of course considerably skewed, because the failure rates for many categories of transformer were inflated by the false failures produced by the data collection method, while for some categories where the population size was small the failure rates were either extremely small or extremely high.  These small-population failure rates were not representing actual failure rates, but instead were just demonstrating the “luck of the draw” that occurs with small sample sizes.  If a category has just 4 transformers, and none has failed during the past 10 years, the failure rate is zero, whereas if one has failed, the failure rate is 2.5%.  This result can occur regardless of whether the actual failure rate is 1%, 2% or any other value.

Summary

Spare transformers play an important role in making it possible to achieve high levels of service reliability.  The considerations are somewhat different between the transmission and distribution systems, but the proper analysis methods are similar.  Application of the Binomial Probability Distribution Function (BPDF) allows for direct computation of the various system states’ probabilities, and allows for prediction of the degree of improvement achieved with the addition of each spare.

For example, suppose that we have a fleet of 25 similar transformers with a failure rate of 0.8% per year.  If the outage duration is ordinarily 1 year, but reduced to 1 month if a spare is available, the probability of being in the various system states is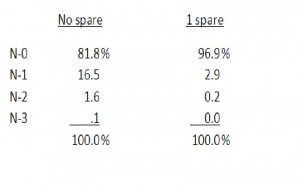 

It is possible to compute revised probabilities for the scenarios of adding one, two, three, or any number of spares to the fleet.  One can then scientifically make informed statements regarding the incremental reliability improvement achieved with addition of each spare, and compare this to the cost of each spare.

The BPDF method requires only knowledge of the failure rate, and the number of transformers in the population.  It does not require purchase of, and training on, esoteric mathematical modeling programs.  Rather, it only involves use of one algebraic formula.  Consequently, it is an elegant and mathematically-defendable method of analyzing the spare transformer topic.

Although many more-complex methods of analysis can be formulated, these alternative methods are unnecessarily difficult to understand, and can easily produce erroneous results, especially if they are based on incorrect understanding of the physical realities associated with transformer fleet management.

R Gonzalez, PE